数据
数据获取
数据集来源:
- MNIST:手写数据集
- ImageNet:图片数据集
- AudioSet:youtube上的声音切片
- Kinetics:youtube上的人行为视频切片
- KITTI:无人驾驶中传感器的数据集
- Amazon Review:亚马逊的用户评论
- SQuAD:维基百科上的问答对
- LibriSpeech:1000小时的有声读物
数据集网站:
- paperswithcode:学术常用数据集
- kaggle:数据科学家上传的机器学习数据集
- google dataset search:谷歌搜索数据集
- tensorflow:工具包数据集
- huggingface:专注于做文本的transeformer数据库
- Open Data on AWS:大规模原数据
生成合成数据:
爬网页数据:
数据标注
数据分析
数据清理
数据变换
特征工程
机器学习简单算法
机器学习介绍
机器学习分为:
- 有监督学习 Supervised:数据有标号,模型来预测标号
- 半监督学习 Semi-supervised:有一些数据有标号,但也要使用无标号的数据
- 无监督学习:数据没有标号,模型的任务也不是去标号
- 强化学习:利用与环境交互的观察结果采取行动而获得最大化的奖励
损失函数 Loss:模型预测值和真实值的差距的一类型函数
目标函数 Objective:将损失函数最小时的模型各参数
模型优化 Optimization:解出目标函数的算法
有监督机器学习的模型分类:
- 决策树 Decision trees
- 线性模型 Linear methods
- 核方法 Kernel machines:使用核函数来衡量两个样本的相似度
- 神经网络 Neural Networks:用神经网络来学习特征的表示
决策树
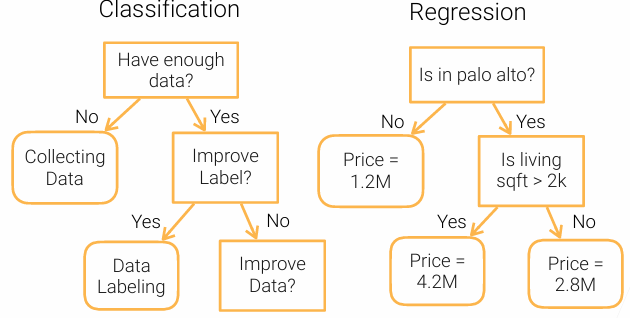
优点:
- 可以被解释
- 可以处理数值类或类别类的特征
缺点:
- 不稳定(易受噪音影响)
- 导致过拟合(树枝太多了)
- 不好在并行计算的GPU上进行部署(性能上吃亏)
缺点的解决方法:
- 随机森林 Random Forest(解决不稳定):独立训练多棵树,将结果投票或取。随机指的是在每一棵树的训练过程中,数据是从数据集中随机选取的,可能重复选中也可能选不到。而且树的特征选取也是随机的
- 梯度上升决策树 GBDT
初始化:首先,GBDT会用一个简单的模型(如常数模型)对所有样本做出初始预测。 迭代过程:
- 计算残差:基于当前模型的预测结果,计算每个样本的真实标签与预测值之间的梯度(对于回归问题通常是真实值减去预测值;对于分类问题,则使用损失函数的负梯度)。
- 拟合决策树:将这些残差作为新的目标变量,训练一个决策树来拟合这些残差。决策树的深度和节点数决定了模型的复杂度。
- 更新预测:将新训练的决策树加入到模型中,更新每个样本的预测值为原预测值加上新决策树的输出。
支持向量机 SVM
SVM 的目标是找到一个超平面(在二维空间中是一条直线,在三维空间中是一个平面),使得:
-
超平面能够将不同类别的数据分开。
-
超平面与最近的数据点(支持向量)之间的距离(即“间隔”)最大化。
假设数据是线性可分的,SVM 的目标是找到一个超平面: \(\mathbf{w}^T \mathbf{x} + b = 0\) 其中:
- $\mathbf{w}$是超平面的法向量。
- $b$ 是偏置项。
- $\mathbf{x}$ 是输入特征向量。
分类决策函数为: \(f(\mathbf{x}) = \text{sign}(\mathbf{w}^T \mathbf{x} + b)\)
- 如果 $f(\mathbf{x}) > 0$,则属于正类。
- 如果 $f(\mathbf{x}) < 0$,则属于负类。
线性模型
对于预测问题,当数据的特征$x_1 x_2 …x_n$,线性模型的预测结果为$y = w_1x_1+w_2x_2+…+w_nx_n+b$
目标就是优化平均均方误差 MSE
\[J(w,b) = \frac{1}{n}\underset{i=1}{\overset{n}{\Sigma}}(y_i-<x_i,w>-b)^2\]参数获取的过程(随机梯度下降 SGD):
首先随机初始化$w_1$
然后将t从1,2,…按如下进行迭代,直到参数收敛:
随机采取样本$I_t\subset{1,…,n}$且$|I_t| = b$(这里b是每次选取样本数量大小,每次使用的小批量 mini-batch)
更新$w_{t+1} = w_t-\eta_t\nabla_{w_t}l(X_{I_t},y_{I_t},w_t)$
即:
\[w_{t+1} = w_t - \eta \frac{\partial J(w_t, b_t)}{\partial w}\] \[b_{t+1} = b_t - \eta \frac{\partial J(w_t, b_t)}{\partial b}\]其中,$\eta$为学习率,J为损失函数
对于分类问题,输出的就是一个类别。假设实际类别为 $[y_1,y_2…y_m] (y_i = 1\ if\ i=y\ otherwise\ 0)$计算方法为先计算各个类别的置信度$o_i = <x,w_i>+b_i$(用预测的方法计算)然后通过如下方法进行分类:
- softmax算子 来将置信度转化为方便决策的 概率 形式:
衡量正确预测的概率:
\[H(y,\hat y) = \underset{i}{\overset{}{\Sigma}}-y_ilog(\hat y_i) = -log\hat y_y\]