深度学习笔记

神经网络

神经网络一定意义上可以说是代替人进行的数据特征提取

多层感知机 MLP

多层感知机中最重要的概念是 全连接层 dense layer 。在该层中有可以学习的参数$W\in R^{m\times n},b\in R^m$。输入通过全连接层将输出结果$y = Wx+b\in R^m$

这里可以借助线性模型理解：线性模型就是输入维度为1（即一个向量）通过全连接层的结果。将其扩展成含有m个特征的n个数据可输出n个结果组成的向量

如上的模型也只停留在线性阶段。要引入非线性，需使用 激活函数 ：

通过全连接层和激活层的交替，就实现了多层感知机算法

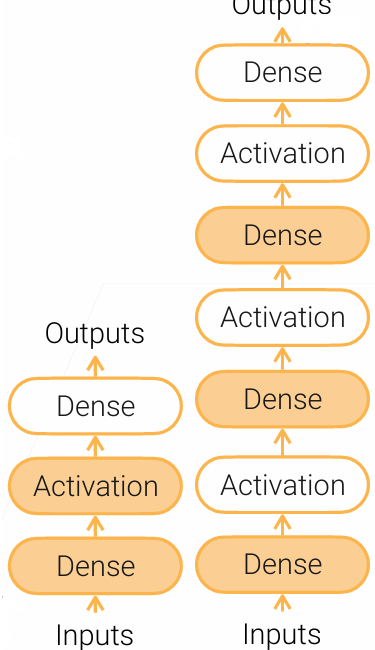
与输出不相连的全连接层就是 隐藏层 ,最后一个全连接层叫做 分类层

卷积神经网络 CNN

CNN实际上是从MLP中的全连接层过渡到 卷积层 。卷积的产生：由于当输入和输出的特征特别多时（如图片，具有很多很多像素），需要学习的参数太多（全连接层输出和输入的乘积）。而在这样的应用中通常具有如下两个性质：

• 平移不变性：如图像类别识别中，要识别的特征位置发生平移也一定能识别到

• 本地性：离得近的像素相关性就高，不需要找离得远的像素

卷积就是利用了这两个性质。通过 卷积核 kernel 与对应的像素进行卷积，替代了原本庞大的权重矩阵与输入进行乘积，这样可学习参数个数只与卷积核大小k相关了，减小了学习成本。

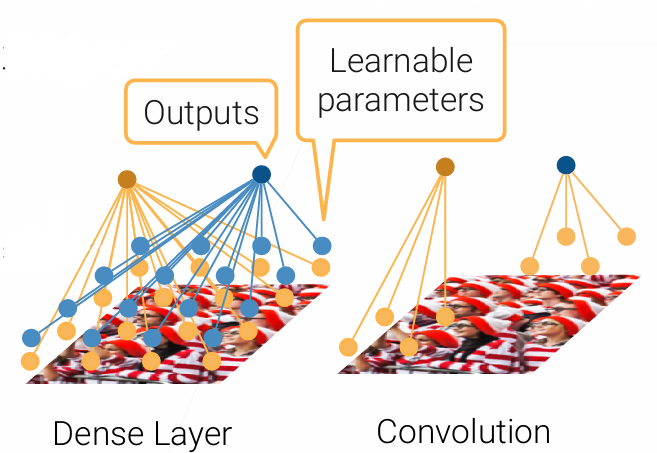
单核卷积神经网络的实现方式：

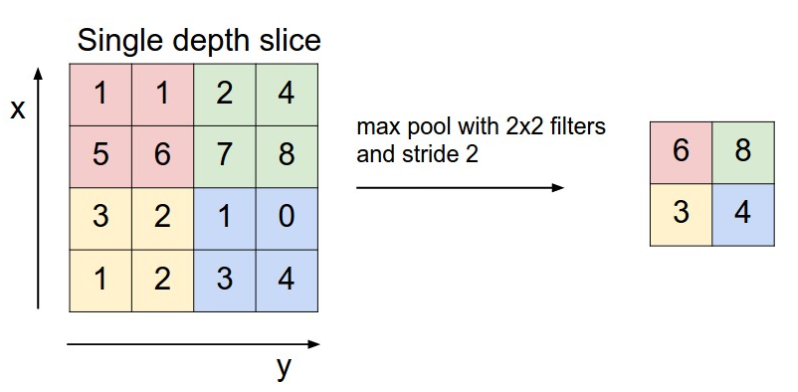
在卷积计算之后，输出的大小仍然没有改变，在这样的一张记录所有输出的矩阵图中，存在着很多无用信息（即经过卷积计算后仍然较小的数，这代表着与特征的相关性不高），因此需要一个新的层来将无用信息删除掉。这样就诞生了 池化层 pooling layer。其作用主要是降维、去除冗余信息、减少下一层的计算量等。

池化分为 最大池化 max pooling和 平均池化 average pooling。下图展示的是最大池化，平均池化就望文生义了。此外还有重叠池化 overlapping pooling（相邻窗口之间有重叠区域）、空金字塔池化 Spatial Pyramid pooling（不细说）

卷积神经网络 CNN 就是将卷积层、激活层、池化层一层一层堆叠起来，最后连着一个分类层获得输出的算法。

区域卷积神经网络 R-CNN

该算法采用以下步骤：

• 使用启发式的搜索算法选择锚框
• 用预训练模型来搜索特征。
• 训练一个支持向量机 SVM 来对类别分类。
• 训练一个线性回归模型来预测边缘框偏移。

对于一个大小不定的选中的锚框，要输出一个大小固定的$n\times m$的batch，使用的是 兴趣区域 Rol 池化层。

兴趣区域池化层就是给定一个锚框，均匀分成$n\times m$块，输出每块里的最大值（若该元素被切开了，只要在块里就算）。

Fast R-CNN：改进版R-CNN。不再对于候选区域单独提取特征，而是对整个图像提取特征，然后通过兴趣区域池化层从特征图提取特征（通道数等于原本候选区域数）。这样将分类和边界框回归整合到一个网络中，实现端到端训练。提高了训练和推理速度、减少了存储开销。

Faster R-CNN：再改进版。用一个神经网络 区域提议网络 RPN 来进行锚框的生成（本质上就是卷积神经网络）。然后使用 非极大值抑制 NMS来筛选出高质量的锚框，后面就跟R-CNN一样。

Mask R-CNN：再再改进版。能达到像素级别的标号。

单发多框检测 SSD

总体思想就是对于给定的图像的每个像素，都生成多个以它为中心的锚框。给定n个大小和m个宽高比（生成n+m-1个锚框）。首先，输入图像经过一层基础网络，然后进行锚框生成、特征检测等，然后再经过卷积层块来减小宽高（通常是减半），进行锚框生成、特征检测，然后再经过卷积层块…以此类推。如图所示，上层通常检测大目标，下层检测小目标。

循环神经网络 RNN

对于自然语言模型，通常是进行预测，即给定一个单词和语境，预测下一个单词。若使用MLP算法，输入的维度是不能发生变化的，即我只能依靠当前的单词来预测下一个单词，不能结合之前的语境。因此RNN算法就是解决非固定长度输入的。

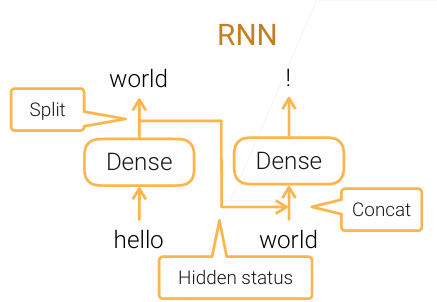
这里RNN模型经过第一个全连接层后的结果包含了输入的信息，在经过Split运算后与下一个循环进行Concat运算，这样就实现了最开始输入信息的传递（hello）。下面是一个最简单的RNN：

这里每一层循环都经过两个输入：一个当前时刻输入$x_t$，一个包含上一时刻信息的隐藏态$h_{t-1}$。在当前时刻的输出$y_t$复制一份以隐藏态$h_t$。这里$y_t$和$h_t$本质上是一个东西（在此简单版本中）。

复杂一点的RNN含有 门 Gated RNN，如LSTM、GRU。会选择性抑制一些输入，如语言模型中对于介词等词汇会选择忘掉$x_t$，当新的一段开始时会忘掉前一段一些信息$h_{t-1}$，这些忘掉信息的参数也是通过学习的。

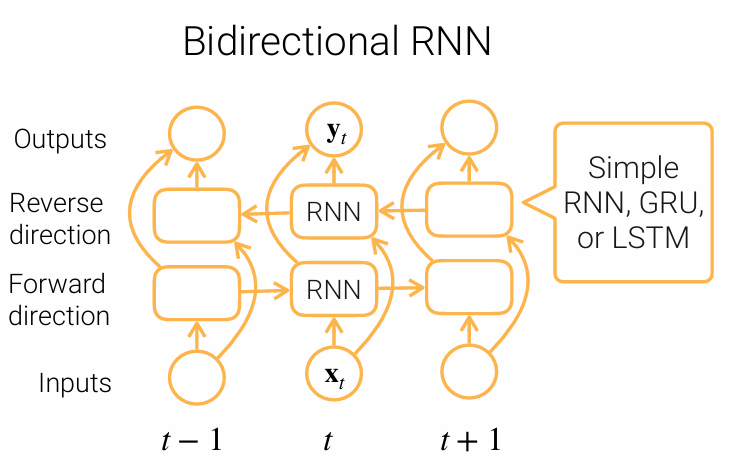
为了适应句子方向的左右需求，即有时需要理解整个句子的语义，产生了双向RNN Bi-RNN。双向RNN存在着反向时时刻t+1的输出作为隐藏状态作用于时刻t的全连接层。这样的算法可以更好适应整个语境的信息，如做完形填空的时候。

Seq2seq

此模型用于处理序列到序列的问题，例如文本翻译等。

Seq2seq是一个 编码 Encode 解码 Decode 架构。编码器是一个RNN，读取输入句子（可以是双向），解码器是另一个RNN用于输出。编码器将最后的隐藏状态（包含句子所有的信息）传给解码器

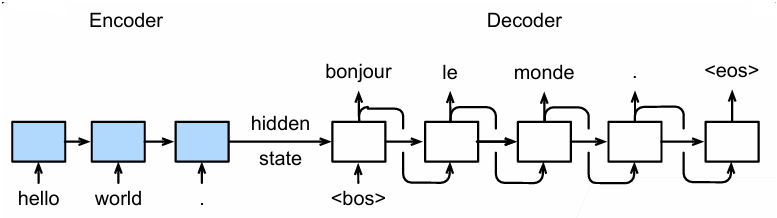
解码器在训练和推理的时候输入不同。在训练的时候，输入的都是正确的目标句子，而在推理的时候的输入是上一循环推理出的结果。

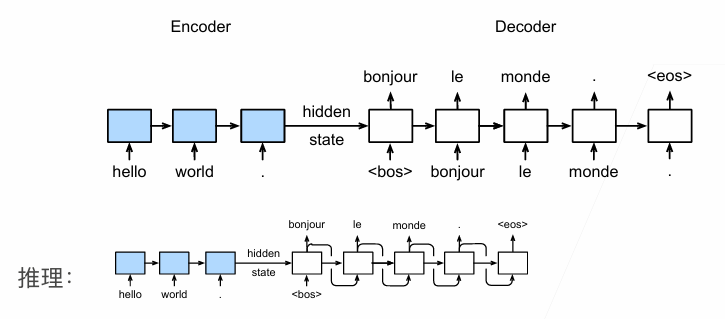
seq2seq中层的表示如下：

为衡量生成序列好坏，采用了 BLEU，定义如下：

其中，p_n是预测中所有结果的精度。假如预测结果是ABBCD，正确结果是ABCDEF，则$p_1 = 4/5,p_2 = 3/4,p_3 = 1/3,p_4 = 0$,n代表预测结果中连续的n个单元，$p_n$代表匹配的数量占总量的比例

BLEU最大值为1，此时为完美预测。这里前一段的指数项用于惩罚过短的预测，而后一段表现为长的匹配具有高权重（即如果长匹配过少，就狠狠惩罚）

引入注意力机制的 seq2seq

在上述的seq2seq中，编码器输出的隐藏层进入解码器的输入，这一隐藏层包含的是整个句子的整体信息，但是对于特定字节（即循环到的特定位置），理论上应对应于一些原始字符，这应当被注意（举例：英文翻译时一些英文单词对应中文的一些词语更加合理）。原本的seq2seq无法对此直接建模，因此便引入了 注意力机制。不说人话的话就是原本的模型存在信息瓶颈（上下文易丢失细节）和难以捕捉长距离依赖问题

实现方式如下

对于解码器的输入，除了原本的嵌入层 Embeding 和编码器输出的隐藏态（二者concat一起）之外，增加了一些。

• 将编码器对每次词的输入作为key和value（key和value是等价的一对）放进Attention里面
• 解码器RNN对上一词的输出是query也放进Attention里
• Attention的输出和下一个词经过嵌入层的结果合并（concat）进入下一个循环的解码器RNN

这里键就是编码器的隐藏状态，姑且先认为键和值是一个东西。而查询就是解码器的隐藏状态。这里用形象的比喻：

查询Query问注意力层：“我现在需要生成一个词，我这里有输出上一个词包含语义的特征”

键Key告诉注意力层：“截至目前，输入序列的每个部分都有这些信息，你可以根据需要选择。”

注意力层告诉解码器：“比较查询和键给我的输入，他们的相似度打分经过softmax归一化后,我将这个结果和值Value进行加权求和了，给你这个生成的上下文向量”

注意力机制可以如下表示：

变换神经网络 Transformer

自注意力

自注意力池化层是将给定序列$x_1,x_2,…,x_n$当作key、value、query来对序列抽取特征得到$y_1,y_2,…,y_n$。这里：

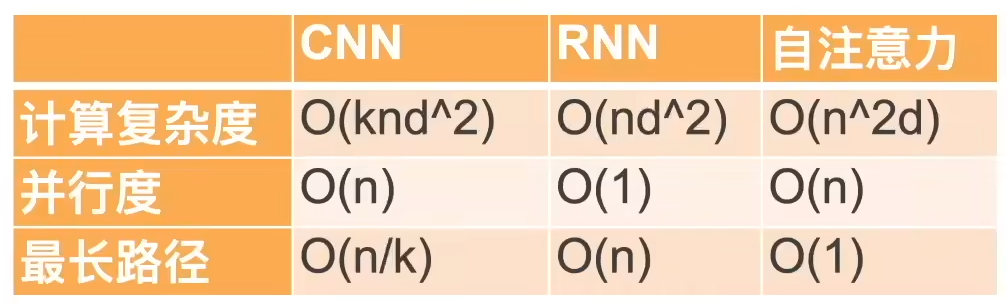
下面是三种模型的对比（n是序列长度，d是一个token特征向量的长度，k是卷积核大小）

自注意力机制可以如下表示：

其中，$Q = XW_Q,\ K = XW_K,\ V = XW_V$，三个都是输入向量乘对应的参数矩阵

由于自注意力机制没有记录位置信息（与CNN、RNN不同），如果没有位置信息输入的语序都是乱的也能训练出来模型输出肯定在胡言乱语。因此引入一个位置编码将位置信息灌入输入中。假设输入序列长度为n，$X\in R^{n\times d}$，那么位置编码矩阵为$P\in R^{n\times d}$，输入就改为$X+P$(相加这个挺玄学的反正)。P中的元素计算如下：

至于为什么要这样设计，是因为这样两个词之间通过线性变换投影后相对位置不变。我们通常只关注句子中词的相对位置，不关注绝对位置，因此这样是合理的。

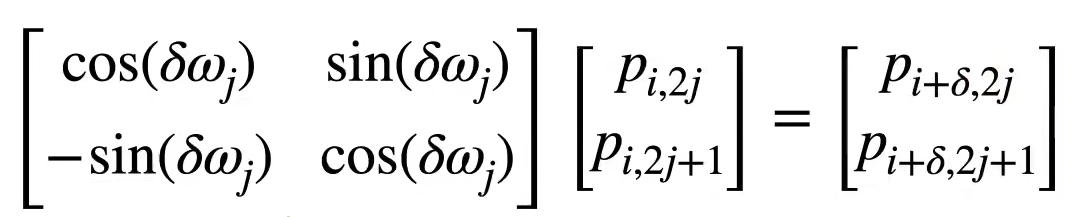
Transformer 架构

Transformer仍然使用编码器-解码器架构和注意力机制，但与seq2seq不同的是，Transformer是纯基于自注意力的架构（没有RNN）。

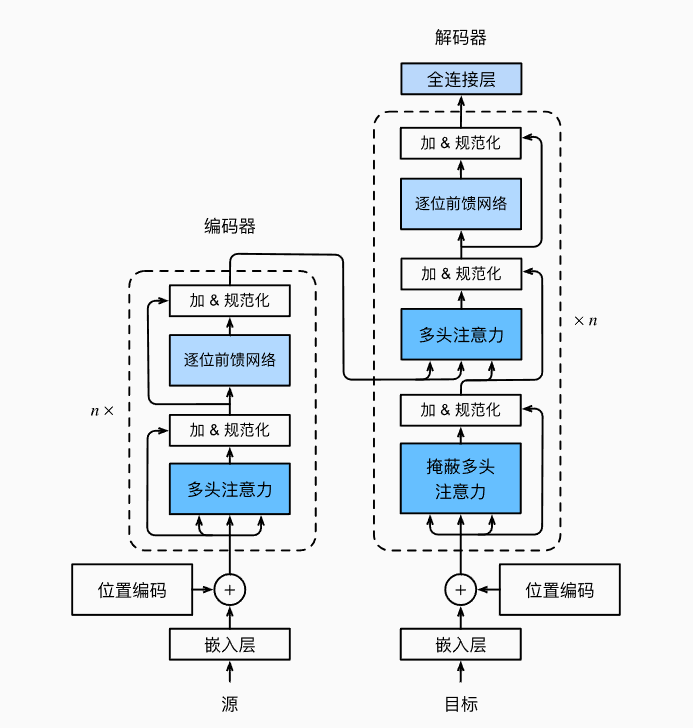
图中的 加&规范化 就是一个全连接层。这里面左边虚线框里的东西叫做一个Transformer块。

所谓的多头注意力是指：对于同一组Key Value Query，采用多通道的注意力运算后用concat运算并起来。有点类似于卷积神经网络中的多通道识别

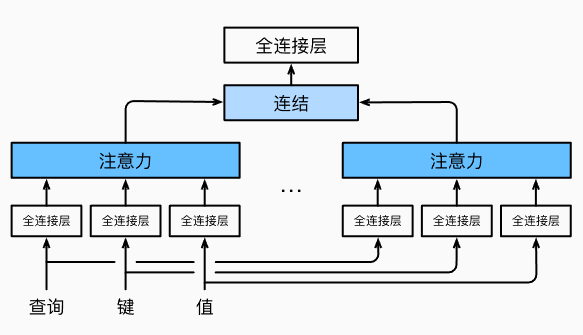
看一下多头注意力可学习参数的维度

对于$q\in R^{d_q}, \ k\in R^{d_k},\ v\in R^{d_v}$

头i可学习的参数$W_i^{(q)}\in R^{p_q\times d_q},W_i^{(k)}\in R^{p_k\times d_k},W_i^{(v)}\in R^{p_v\times d_v}$

头i的输出$h_i = f(W_i^{(q)}q,W_i^{(k)}k,W_i^{(v)}v)$

输出的可学习参数$W_o\in R^{o_o\times hp_v}$

多头注意力的输出为

有掩码的多头注意力是指：解码器 对序列中一个元素输出时，不应该考虑之后的元素，即计算$x_i$时，假装当前序列长度为i，将之后的忽略

所谓的 基于位置的前馈网络 FFN 是指：对于多头自注意力层的输出向量$X=(x_1,…,x_n)$对每一个$x_i$都进行一次全连接层计算。由于每一个$x_i$代表着位置不同的词，因此称为基于位置。输入时形状由$(b,n,d)$变换成$(bn,d)$（第一个全连接层），然后激活，输出时形状由$(bn,d)$变换回$(b,n,d)（第二个全连接层）$。这样的作法就是因为将位置有关的变量b和n（b是批量大小，n是序列长度）整合到一起，方便对每个位置进行非线变。

层归一化 ：这一层有两个输入，首先将这两个输入直接加和（$X_1+X_2$,其实这里本质上是一个残差，因为是多头注意力层的输出与输入之间的加减）。然后进行层归一化，层归一化（不是softmax算子）公式如下（这里$\mu 、\sigma$分别是特征向量的均值和方差，$\epsilon$就是很小的一个数，为了避免除0错误）：

信息传递 ：编码器的输出为$y_1,…,y_n$，将其作为解码器中国第i个Transformer块中多头注意力的key和value（它的query来自目标序列）。这里下面的两个多头注意力都是自注意力，但是上面的多头是普通注意力。一位置编码器和解码器中块的个数和输出维度是一样的。

生成模型

生成对抗网络 GAN

生成对抗模型由 生成器G 和 辨别器N 组成。生成器输入噪声，输出生成的数据（目标是生成真实的数据）。辨别器输入生成的数据，输出该数据的真实性概率（目标是区分真假数据）。

生成器：输入一个均值为0的高斯噪音z，生成器就是一个参数可学习的映射（神经网络模型，可以是MLP）将输入映射为x。可学习的参数为$\theta_z$

辨别器：辨别器也是一个参数可学习的映射，可学习的参数为$\theta_d$，输出一个标量在 0~1 之间。如果数据是真实的，标量为1；假的就是0。本质上是一个二分神经网络

训练过程：训练生成器使得 这个数：$\log(1-D(G(z)))$ 最小。也就是让生成出来的数据十分的真实，就是尽可能让辨别器出错，使之不能判断出生成出来的数据是否真实。训练的目标函数如下：

这里x是真实的数据，G(z)是生成的数据。如果辨别器是完美的话，则两个log里面的项都是1，则整个等于0。而对于生成器则如果是完美的话，则后面那一项会是负无穷。

关于迭代的方法，这里放上原论文中的内容：

图神经网络 GNN

简单的图神经网络：对于每个节点V、边E、全局属性U都用一个MLP连接其所相连的同种成分（一个GNN层），通过多个GNN层构成GNN

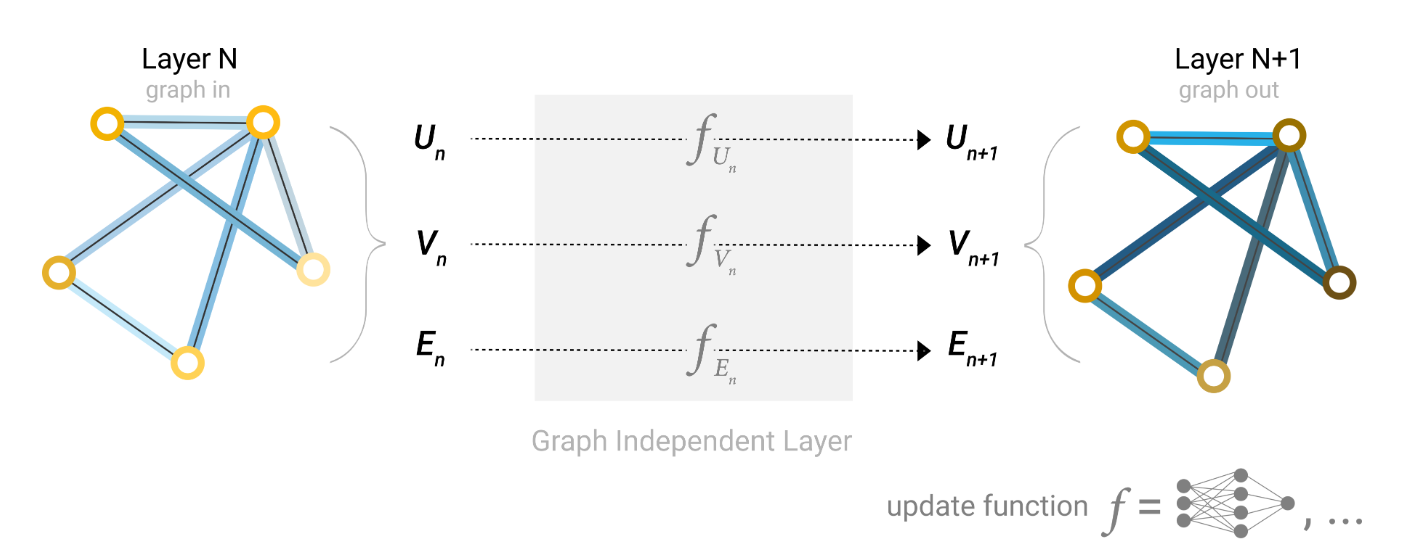
包含池化的图神经网络：对于每个节点，如果想提取边的信息，将邻接边的特征向量聚合成一个矩阵，然后进行求和操作。通过节点来求边也是一样的。通过节点的属性也可以预测全局属性U（通过全局平均池化层 ）

进一步，消息传递可以同时发生在节点和边上，由于边与节点特征向量不一定相同，因此需要进行线性变换

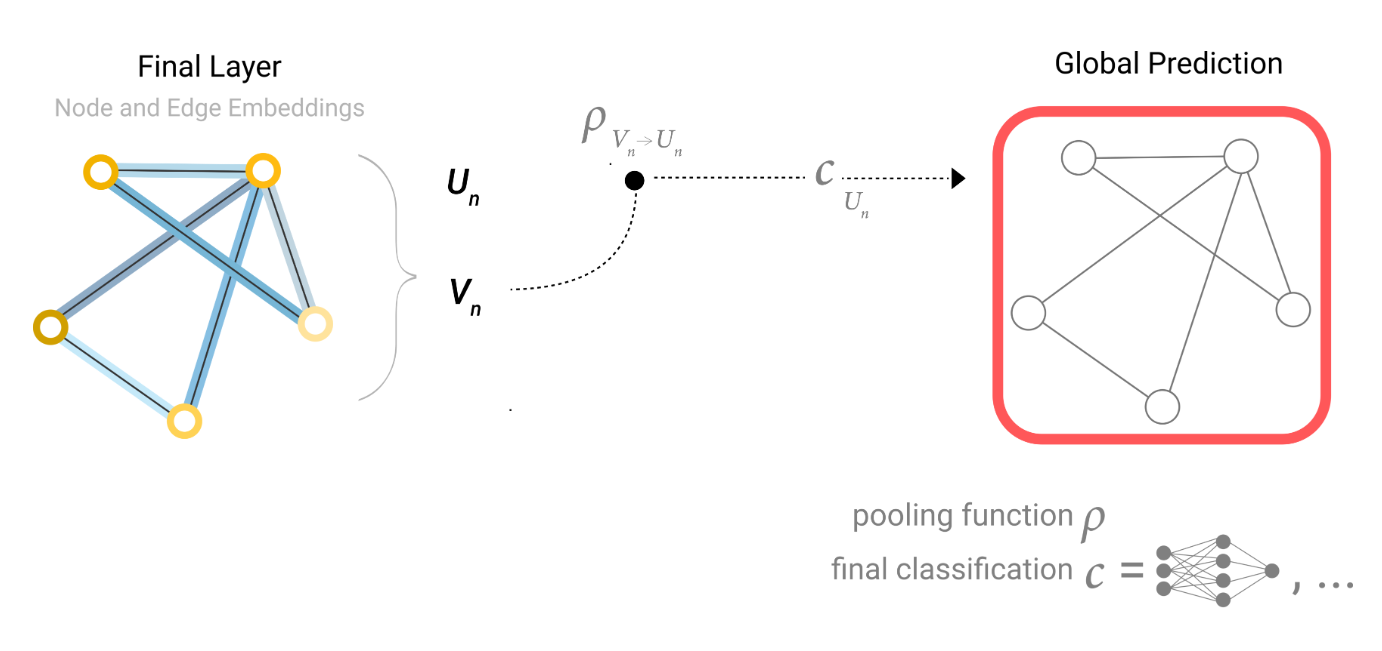
但这样的话先更新边还是先更新节点成了一个问题，因此可以采用如下几种方式：

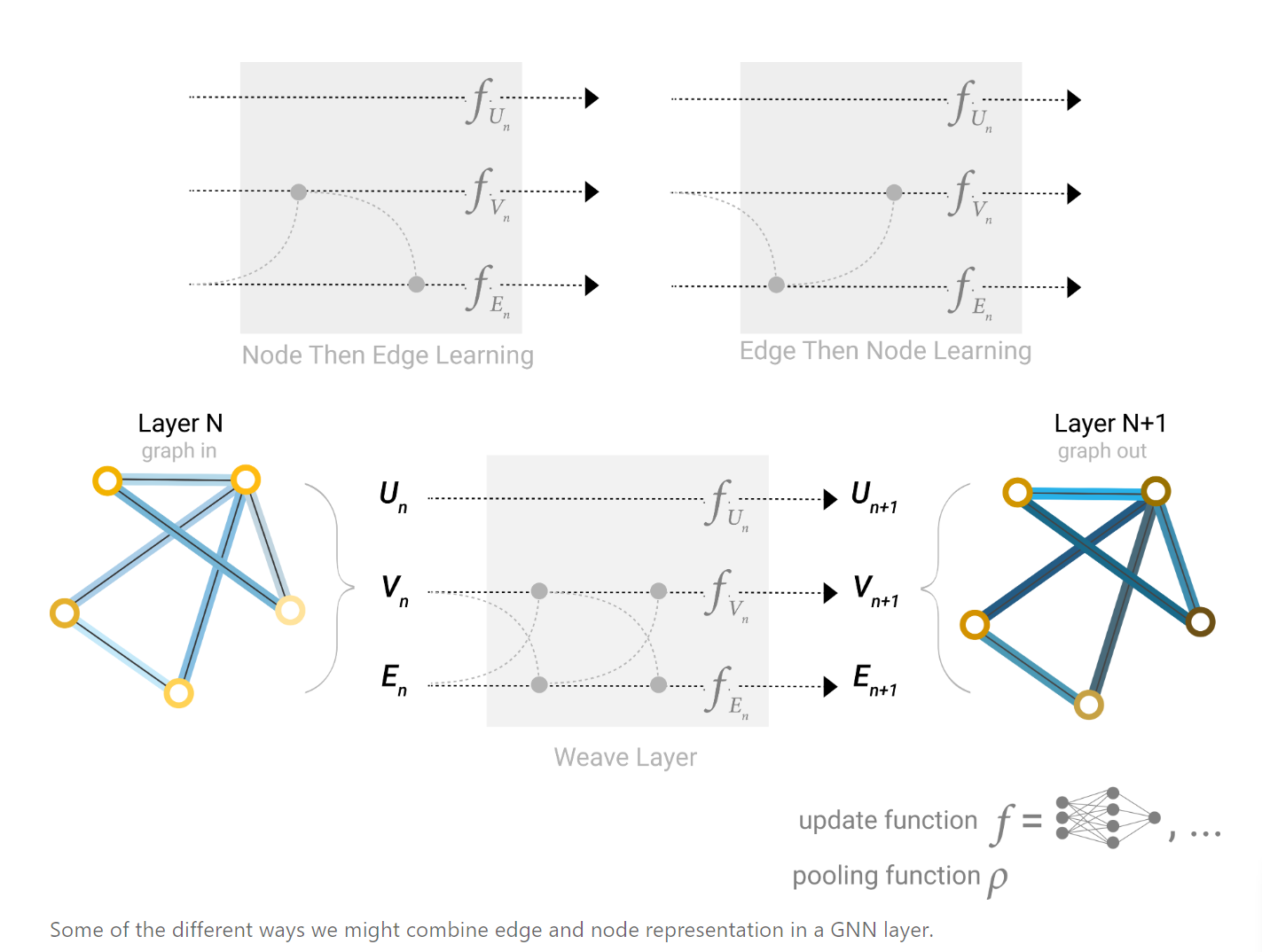
或者使用图的全局表示或上下文向量。就是将全局表示中融合了所有节点和边的信息（一个特殊的向量），融合方式包括拼接、线性映射、特征调制层（类似于注意力机制）

• 新章
  实用机器学习
• 旧篇
  强化学习导论