强化学习导论

多臂赌博机问题

评估是相对指令而言的。教导式学习的反馈通常是给定什么指令是正确的，而评估式学习的反馈是给定行为的得分。

定义$q_*(a)$是给定选择a的预期奖励。则：

\[q_*(a)\dot =E[R_t\|A_t = a]\]

用$Q_t(a)$表示在t回合时动作a的估计奖励。我们希望$Q_t(a)\rightarrow q_*(a)$。若在t回合之前行为a被选了$k_\alpha$次，产生了$r_1,…,r_{k_\alpha}$的汇报，则估计行为值为：

\[Q_t(a) \dot= \frac{r_1+...+r_{k_\alpha}}{k_\alpha}\]

$k_\alpha = 0$时，令其默认值$Q_0(a) = 0$,当$k_\alpha$无限大时，由大数定律，$Q_t(a)$收敛到$Q^*(a)$

下面时两种选择规则：

贪婪算法：每回合都选最高行为值的行为
$\varepsilon-greedy$算法：大部分回合以贪婪算法，但以小概率$\varepsilon$选择一个均匀的、独立于行为估计值的随即行为。

下图是原书在概念上区别的通俗解释。

对于行为值方法，若回合无限多，则需要的内存也是无限多。因此采用如下的 增量式 实现：

\[Q_{n+1} \dot= \frac{1}{n}\underset{i=1}{\overset{n}{\Sigma}}R_i = Q_n + \frac{1}{n}[R_n-Q_n]\]

对于如上公式，采用如下演化，以适应一个非稳态的情况。

\[Q_{n+1} = Q_n + \alpha[R_n-Q_n]，\ 0<\alpha\leq1\]

这里将$\frac{1}{n}$变成了$\alpha$，导致不同时期奖励的权重发生变化，即权重根据$1-\alpha$的指数呈指数衰减。

书上提到的步长就是$\alpha_n(a)$参数。随机逼近理论提供保证收敛的条件为：

\[\begin{align*} & \underset{n=1}{\overset{\infty}{\Sigma}}\alpha_n(a) = \infty \ 和 & \underset{n=1}{\overset{\infty}{\Sigma}}\alpha_n^2(a) < \infty&& \end{align*}\]

下面介绍另一种动作选择算法：上置信区间 UCB

\[A_t \dot= \underset{a}argmax\left[Q_t(a) + c\sqrt{\frac{\ln t}{N_t(a)}}\right]\]

argmax是当[]的内容取最大值时对应自变量a的值
$N_t(a)$表示在时间t之前选择动作a的次数
c 表示控制探索的程度（说是通常设置为2）
平方根项是对一个值估计的不确定性或方差的度量
总体思想就是后面那一项与这个动作被探索的程度（做过的次数）有关，鼓励开发一些没被探索的动作

说是这个算法在k臂赌博机效果比 $\varepsilon-$贪婪算法更好一点，但是难以处理非平稳问题和大状态空间时的问题

class UCB:
    def __init__(self, n_arms, c=2):
        self.n_arms = n_arms
        self.c = c
        self.Q = np.zeros(n_arms)  # 动作的估计收益
        self.N = np.zeros(n_arms)  # 动作的选择次数
        self.t = 0  # 总步数

    def select_action(self):
        # 计算 UCB 值
        ucb_values = self.Q + self.c * np.sqrt(np.log(self.t + 1) / (self.N + 1e-5))
        return np.argmax(ucb_values)

    def update(self, action, reward):
        # 更新动作的选择次数和估计收益
        self.N[action] += 1
        self.Q[action] += (reward - self.Q[action]) / self.N[action]
        self.t += 1

到此对每个特定的动作没有特定的偏好，下面就要对动作加上偏好，表示为$H_t(a)$。需要解释的是：

偏好是相对的
偏好与奖励无关

在偏好影响下，动作概率 遵循softmax分布：

\[Pr\{A_t = a\} \dot= \frac{e^{H_t(a)}}{\sum^k_{b=1}e^{H_t(b)}} = \pi_t(a)\]

$\pi(a)$是选择动作a的概率。通过动作概率的方式，可以平衡了动作探索和回报更大两者之间的关系

def softmax_prob_choose(H)
    exp_H = np.exp(H - np.max(H))
    action_probs = exp_H / np.sum(exp_H)
    return np.random.chioce(len(H), p=action_probs)

动作偏好更新方式如下：

\[H_{t+1}(A_t) \dot= H_t(A_t) + \alpha(R_t - \bar R_t)(1-\pi_t(A_t))\] \[H_{t+1}(a) \dot= H_t(a)-\alpha(R_t - \bar R_t)\pi_t(a)\ , \ for\ all\ a\ \neq\ A_t\]

$\alpha$：步长参数
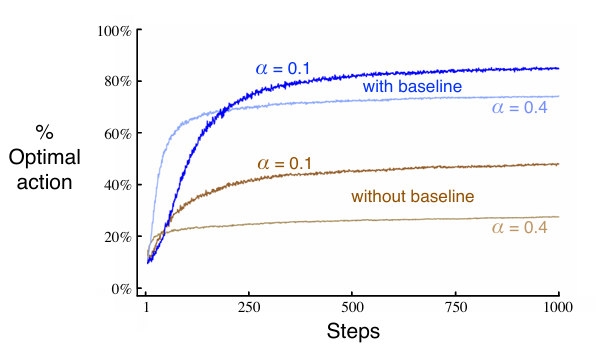
$\bar R_t$：截至回合t的所有奖励的平均值（包含回合t）。称为 奖励基线 Reward Baseline

原文这里说如果去掉了奖励基线（即将其置为0），算法表现大大降低。

到现在为止只考虑了非关联性任务，还有需要将不同行为和不同情况联系起来的任务，如关联搜索任务。

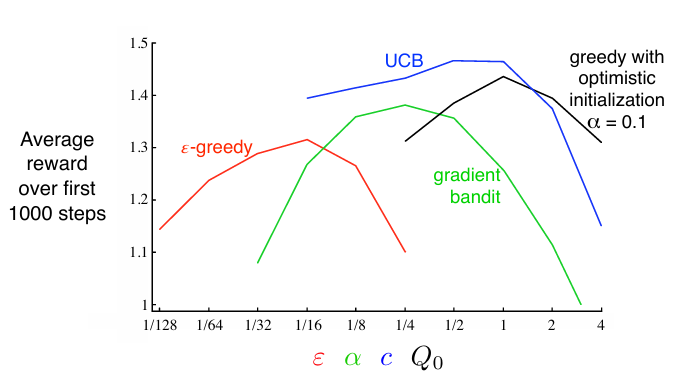
下图是以上提到的几种动作选择算法的比较图：

有限马尔科夫决策过程 Finite Markov Decision Processes

在赌博机问题中，我们估计每个动作的价值$q_(a)$，但在 MDP 中，我们估计关于每个状态中每个动作的价值$q_(s,a)$。

MDP中的学习者和决策者被称为 个体 Agent，其与之交互的东西被称为 环境 environment

MDP中的个体-环境交互

对于每个回合t，个体接受环境状态$S_t$，做出动作$A_t$，收到奖励$R_{t+1}$，达到新状态$S_{t+1}$。

对于给定前一状态和动作的情况下，存在下一状态和回报的概率(联合概率分布)：

\[p(s^′,r|s,a)\dot=Pr\{S_t=s^′,R_t=r|S_{t−1}=s,A_{t−1}=a\}\]

在MDP中，$S_t$和$R_t$的概率仅取决于前一个状态和动作，不依赖于先前的状态和动作的话（状态必须包括有关过去的个体-环境交互的所有方面的信息），就说该状态具有 马尔可夫性 Markov property

通过该联合概率分布可以计算出任何想知道的关于环境的其他信息，如：

状态转移概率 $p(s’|s,a) \dot= \underset{r\in R}{\Sigma}p(s’,r| s,a)$
预期奖励$r(s,a)\dot=\underset{r\in R}{\Sigma}r\underset{s’\in S}{\Sigma}p(s’,r|s,a)$
对下一指定状态的预期奖励$r(s,a,s’)\dot =\underset{r\in R}{\Sigma}r\frac{p(s’,r|s,a)}{p(s’|s,a)}$

目标的定义：目标可以被认为是所接收的标量信号（称为奖励）的累积和的预期值的最大化。

对于一个目标，在最简单的情况下，收益应该为奖励的总和：

\[G_t\dot=R_{t+1} + R_{t+2} + R_{t+3} + ... + R_T\]

当一个任务可以被分解为小任务时，每个小目标被称为 情节 Episodes。因此强化学习任务可以被分成两种：情节任务和连续任务下面是这两个任务的区别：

特性	情节任务（Episodic Tasks）	连续任务（Continuing Tasks）
任务结构	划分为多个独立的情节，有明确的开始和结束	时间步无限延续，没有明确的情节划分
时间范围	有限时间步	无限时间步
回报定义	当前情节内的累积奖励	无限时间步的衰减累积奖励
目标函数	最大化每个情节的累积奖励	最大化长期累积奖励
环境重置	每个情节结束后环境重置	环境不会重置
算法设计	适合蒙特卡罗方法	适合时序差分方法
应用场景	游戏、实验性任务	机器人控制、自动驾驶、资源管理
值函数定义	当前情节内的期望回报	无限时间步的衰减期望回报
策略评估	基于完整情节回报	基于实时交互
探索与利用	可以在不同情节中尝试不同策略	需要在同一任务中平衡探索与利用

在一个任务中，非终了状态的集合为$S$,包括终了状态的所有状态表示为$S^+$，终止时间为$T$。

当存在时间无线的任务时，未来的回报将无法收敛，因此引入了衰减因子$\gamma$。衰减回报为：

\[G_t\dot =R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... + ... = \underset{k=0}{\overset{\infty}{\Sigma}}\gamma^kR_{t+k+1}\]

衰减因子降低了未来奖励的现值使个体更加短视。

下面介绍 策略函数 policy function：如果个体在时间t遵循策略$\pi$，则$pi(a|s)$是如果$S_t = s$，则$A_t = a$的概率。策略函数本质上就是条件概率的集合，将所有的状态映射为每个动作的概率。

在状态为s、策略为$\pi$下的 状态价值函数 state value function 表示为$v_\pi(s)$，是从开始并之后遵循策略$\pi$的预期收益。

\[v_\pi(s) = \dot =E_\pi[G_t\|S_t = s] = E_\pi[\underset{k = 0}{\overset{\infty}{\Sigma}}\gamma^kR_{t+k+1}\|S_t = s]\]

定义策略$\pi$的 动作-价值函数 action-value function

\[q_\pi(s,a)\dot=E_\pi[G_t\|S_t = s,A_t = a] = E_\pi[\underset{k=0}{\overset{\infty}{\Sigma}}\gamma^kR_{t+k+1}\|S_t = s,A_t = a]\]

三者之间的关系为

\[v_\pi(s) = \underset{a}{\Sigma}\pi(a\|s)q_\pi(s,a)\]

即状态价值函数是行动-价值函数在策略下的加权平均。

下面介绍 蒙特卡洛方法 Monte Carlo methods ：是一种估计方法，通过与环境交互，生成完整的情节，利用情节的奖励序列直接估计出值函数（q和v），然后基于估计出的值函数改进策略。这在后面会详细描述。

在强化学习和动态规划中的价值函数满足递归行,因此可以用如下方程表示,称为 贝尔曼方程 Bellman equation,表示了状态价值与下一个状态价值的关系

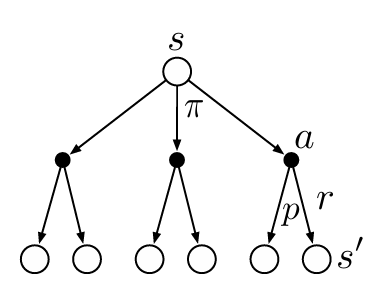
\[v_\pi(s) = \underset{a}{\Sigma}\pi(a\|s)\underset{s',r}{\Sigma}p(s',r\|s,a)[r+\gamma v_\pi(s')]\]

以下图为例，假设当前状态为s，在策略$\pi$下有三个可能的动作，经过这三个动作后在环境的影响下分别可能到达后面的六种状态，导致下一个状态，即$s’$有六种可能。贝尔曼方程就是对所有可能性进行平均，通过其发生的概率进行加权。它指出，开始状态的值必须等于预期的下一个状态的（衰减）值，加上沿途预期的奖励。

同理，动作价值的贝尔曼方程为：

\[q_\pi(s,a) = \underset{s',r}{\Sigma}p(s',r\|s,a)[r+\gamma\underset{a'}{\Sigma}\pi(a'\|s') q_\pi(s',a')]\]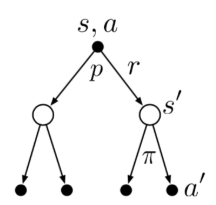

评判一个策略的好坏可以使用策略价值函数。当价值函数取最大值时，此时所采用的策略称为 最优策略，此时的最优策略价值函数为：

\[v_*(s)\dot=\underset{\pi}{\max}q_\pi(s,a)\]

最优策略还具有相同的最优动作价值函数：

\[q_*(s,a)\dot=\underset{\pi}{\max}q_\pi(s,a)\]

在最优的情况下，两个价值函数的贝尔曼方程都具有唯一解，即

\[v_*(s) = \underset{a}{\Sigma}\pi(a\|s)\underset{s',r}{\Sigma}p(s',r\|s,a)[r+\gamma v_*(s')]\] \[q_*(s,a) = \underset{s',r}{\Sigma}p(s',r\|s,a)[r+\gamma\underset{a'}{\Sigma}\pi(a'\|s') q_*(s',a')]\]

均具有唯一解

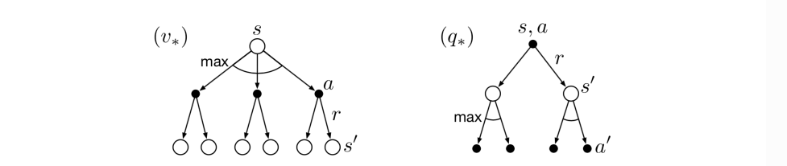
对于有限MDP问题，如果有n个状态，就有n个贝尔曼最优方程。解这个最优方程组，可以获得最优策略对应的最优策略价值$v_$，查询一步（按照价值最大的动作）可以得到最优的决策动作。而计算$q_$甚至能不需要查询动作，最优动作价值直接缓存了查询的结果。从最优策略价值函数获得当前状态的最优策略实现步骤为：

对于当前状态s，便利所有可能的动作a
对于每个动作a，计算其对应的期望价值：

\[Q(s,a) = R(s,a) + \gamma\underset{s'}{\Sigma}P(s'\|s,a)V^*(s')\]

选择使$Q(s,a)$最大的动作$a^*$

多臂赌博机问题

有限马尔科夫决策过程 Finite Markov Decision Processes

目录

标签

伙伴