前言
本文整理了一些关于《现代机器人:力学,规划,控制》(Modern Robotics: Mechanics, Planning, and Control)的轨迹规划部分内容,为机器人学的部分的第四篇笔记,之前的现代机器人学运动学部分在这里,动力学部分在这里
点到点轨迹
轨迹定义为配置空间的曲线,作为时间t的函数,即为$\theta(t),t\in [0,T]$,路径作为路径参数s的函数,即为$\theta(s),s\in [0,1]$。从[0,T]映射到[0,1]称为时间缩放
回顾一下关节空间是配置空间的子集,配置空间表示为广义坐标q,但关节空间用关节变量(关节角和位移)表示。但在这里应该区别不大。
可以求出路径的速度和加速度:
\[\dot\theta = \frac{d \theta}{d s}\dot s\] \[\ddot\theta = \frac{d\theta}{d s}\ddot s + \frac{d^2\theta}{ds^2}\dot s^2\]参数轨迹
直线轨迹包括两种,一种是关节空间的运动为线性的,另一种为任务空间运动为直线。
由于通常关节空间的约束为$\theta_{i,min} \leq \theta_i \leq \theta_{i,max}$,工作空间为凸空间,可以使得关节空间中两点线性轨迹永远在空间内。而任务空间的直线则不一定在空间内。
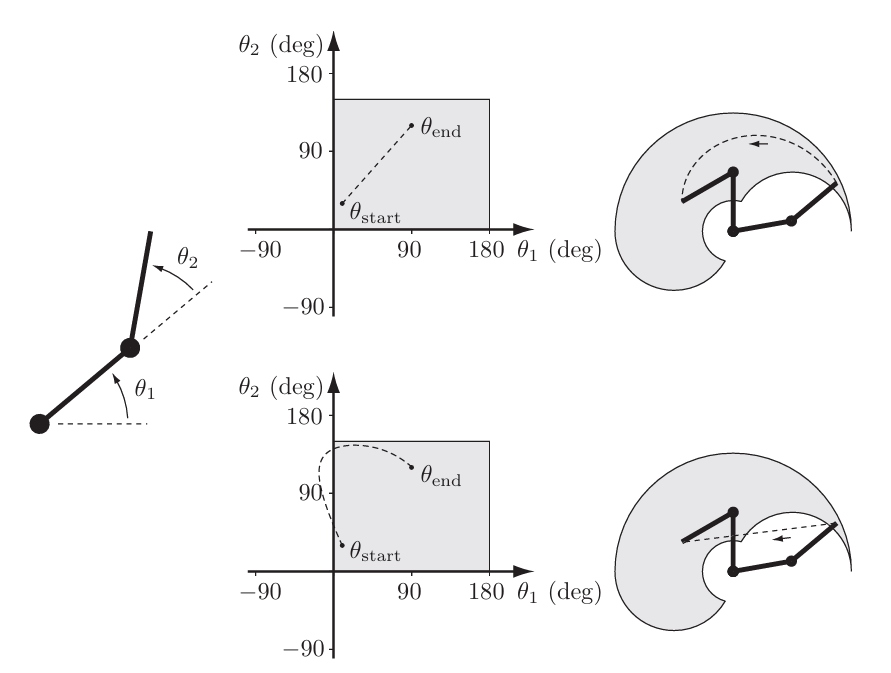
关节空间为线性时,轨迹和速度、加速度如下:
\[\theta(s) = \theta_{start} + s(\theta_{end} - \theta_{start})\] \[\frac{d\theta}{d s} = \theta_{end} - \theta_{start}\] \[\frac{d^2\theta}{d s^2} = 0\]轨迹在任务空间为直线时,路径为:
\[X(s) = X_{start}\exp(\log(X^{-1}_{start}X_{end})s)\]这里$X_{start}$为在坐标系{start}中,起始位置的位姿矩阵。
还有一种旋转和平移解耦的路径生成方式:
\[p(s) = p_{start} + s(p_{end} - p_{start})\] \[R(s) = R_{start}\exp(\log(R^T_{start}R_{end})s)\]这两种生成的轨迹下如图:
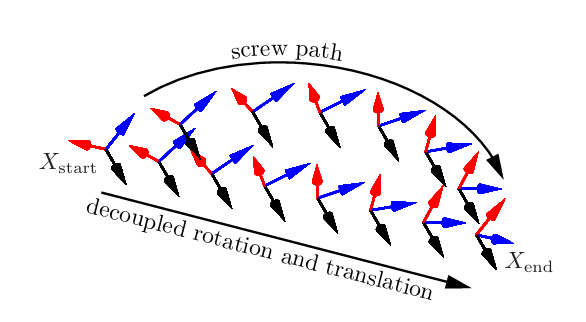
时间轨迹
下面研究真实时间下的时间轨迹,需要将轨迹参数下的轨迹进行时间缩放。一种简单的时间缩放是三阶多项式方式
\[s(t) = a_0 + a_1t + a_2t^t +a_3t^3,t\in[0,T]\]要求这些系数,先求导后代入始末的值。
\[\begin{align*} & s(0) = 0 & \dot s(0) = 0\\ & s(T) = 1 & \dot s(T) = 0 \end{align*}\]得到如下:
\[\begin{align*} & a_0 = 0 & a_1 = 0 & a_2 = \frac{3}{T^2} & a_3 = \frac{2}{T^3} \end{align*}\]如果想让曲线更平滑,可以用五次多项式,这样加速度就不会跳变了。
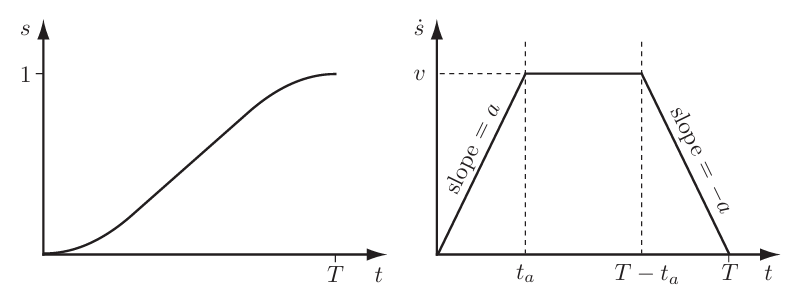
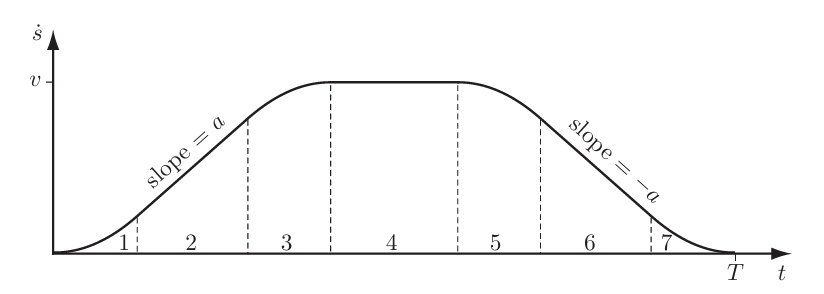
最优轨迹
最优轨迹需结合动力学方程:
\[\tau = M(\theta)\ddot\theta + \dot\theta^T\Gamma(\theta)\dot\theta + g(\theta)\]代入:
\[\dot\theta = \frac{d \theta}{d s}\dot s\] \[\ddot\theta = \frac{d\theta}{d s}\ddot s + \frac{d^2\theta}{ds^2}\dot s^2\]
接下来考虑关节可提供的扭矩:
\[\tau_i^{min}(\theta,\dot\theta)\leq\tau_i\leq\tau_i^{max}(\theta,\dot\theta)\]代入$s、\dot s$,整理获得$\ddot s$的条件:
\[L(s,\dot s)\leq\ddot s\leq U(s,\dot s)\]其中:
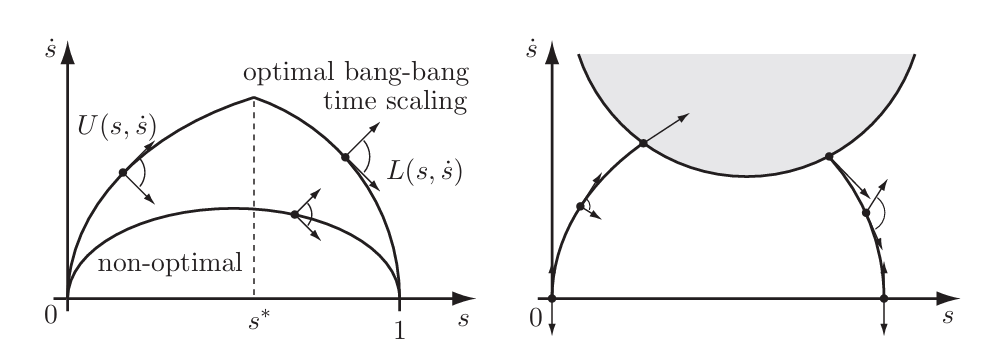
\[L(s,\dot s) = \underset{i}{max}\frac{\tau_i^{min}(s,\dot s)-c(s)\dot s^2-g(s)}{m_i(s)}\] \[U(s,\dot s) = \underset{i}{min}\frac{\tau_i^{max}(s,\dot s)-c(s)\dot s^2-g(s)}{m_i(s)}\]在$s-\dot s$图中,可能的切线方向的最大值和最小值构成了运动锥。最优的时间缩放就是在$s^*$前取最大值U,之后取最小值L,但实际上在中间受到限制,存在一条速度限制曲线,其上方的区域不存在运动锥,因此只能沿着速度限制曲线运动。这样就找到了最优时间缩放
障碍物避让
要实现机械臂的障碍物避让,首先确定机器人的C空间$q\in C\subseteq R^n$:
\[C=C_{free}\cup C_{obs}\]其中,$C_{free}$是机器人不接触任何障碍物的配置集,$C_{obs}$是机器人与障碍物碰撞的配置集。
机器人的状态表示可以为$x=q$或$x=(q,v)\in X$。分别当输入是速度和加速度(或力)的时候。运动方程为:$\dot x = f(s,u),u\in U$
首先对障碍物进行建模。障碍物可以在C空间内表示出来,以一个2R机器人为例。
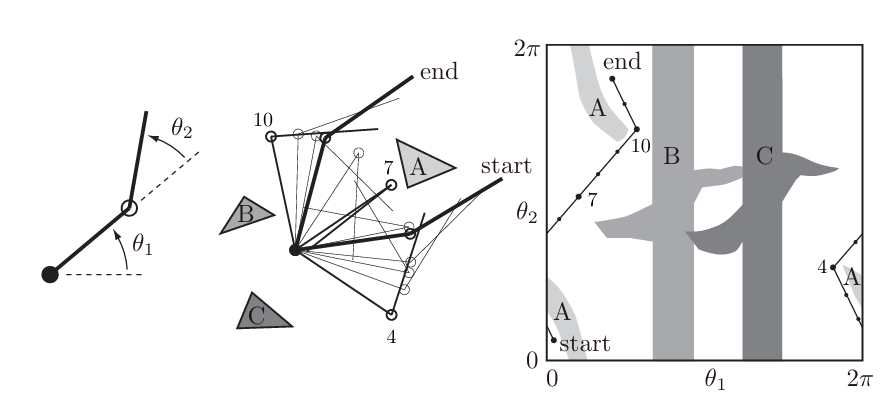
但是这样建模比较困难,尤其是对于复杂的三维障碍物,因此将障碍物转换成一个个球体。
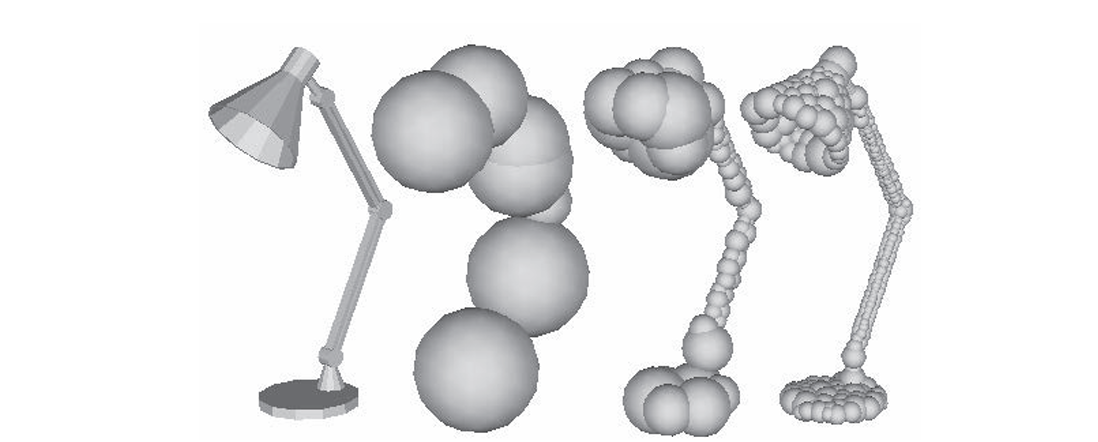
在机器人的$C_{free}$空间内,取一些位置作为节点,每两个节点之间若可达,则连成一条边,这样就构成了一个图。这个路线图具有如下特点:
- Reachability:必须容易或可能找到任何自由配置q和路线图上连线的配置之间的路径。
- Connectivity:在图中的每一个节点都可以通过一定数量的边连到其他任意节点(没有孤立的部分)
制图方法
网格方法
在C空间中,将每个维度切割成k个单元,将C空间网格化,这样障碍物就被以网格表示。
采样方法
PRM图:首先通过均匀随机采样C空间,并在无碰撞时保留该样本。对于每个节点找到附近的k个节点,尝试找到到其的路径(直接画一条线过去),检查路径是否有碰撞,没有碰撞就在这条路径上添加一条边。
RRT图:首先初始化一个树T$x_{start}$(可以为一个节点),然后经过N个如下循环:在状态空间采样$x_{samp}$,寻找T中离$x_{samp}$最近的节点$x_{nearest}$,寻找一个从$x_{nearest}$到$x_{samp}$方向的无碰撞的直线路径作为下一个边,将$x_{new}$添加到T中,如果$x_{new}$在$X_{goal}$中,则返回成功。
RRT是搜索一条从起始点到目标区域一条路径的算法,只能快速提供一条路径,但是很难是最优的。