电阻式传感器
电阻变化和应变关系:
\[\frac{dR}{R} = \frac{d\rho}{\rho} + (1+2\mu)\epsilon\]电阻丝的灵敏度系数:
\[K = \frac{\frac{dR}{R}}{epsilon} = 1+2\mu + \frac{\frac{d\rho}{\rho}}{\epsilon}\]灵敏度主要取决于集合尺寸变化,即以应变效应为主:$K\approx1+2\mu$
对于半导体的压阻效应:
\[\frac{\Delta \rho}{\rho} = \pi\cdot\sigma = \pi\cdot E\cdot\epsilon\]- $\pi$:半导体材料的压阻系数
- $\sigma$:半导体才来哦所受应力
- E:半导体材料的弹性模量
- $\epsilon$:半导体材料的应变
半导体阻值相对变化量:
\[\frac{\Delta R}{R} = (1+2\mu + \pi E)\epsilon\]实验证明,$\pi E$比$1+2\mu$大上百倍,因此后者可忽略,半导体应变片的灵敏度系数为:
\[K = \frac{\frac{\Delta R}{R}}{\epsilon} = \pi E\]半导体材料的应变灵敏度系数一般为金属的50~80倍,但由于 半导体材料的温度系数大,应变时非线性严重 ,使它的应用范围受到一定限制。
下面对电阻应变片进行温度误差补偿,产生温度误差主要因素有两个方面:电阻温度系数影响 和 弹性元件材料和电阻丝材料的线膨胀系数的影响
敏感栅的电阻丝阻值随温度变化的关系可用下式表示:
\[R_t = R_0(1+\alpha_0\Delta t)\]- $R_t$:温度为t时的电阻值
- $R_0$:温度为0时的电阻值
- $\alpha_0$:金属丝的电阻温度系数
- $\Delta t$:温度变化值
弹性元件材料和电阻丝材料的线膨胀系数的影响:
- 当弹性试件与电阻丝材料的线膨胀系数相同时:环境温度变化不会产生附加变形。
- 当弹性试件与电阻丝材料的线膨胀系数不同时:环境温度变化,电阻丝会产生附加变形,从而产生附加电阻变化
电阻丝和弹性元件的线膨胀系数为:$\beta_s$和 $\beta_g$
直流电桥
通过直流电桥来进行应变片的温度补偿

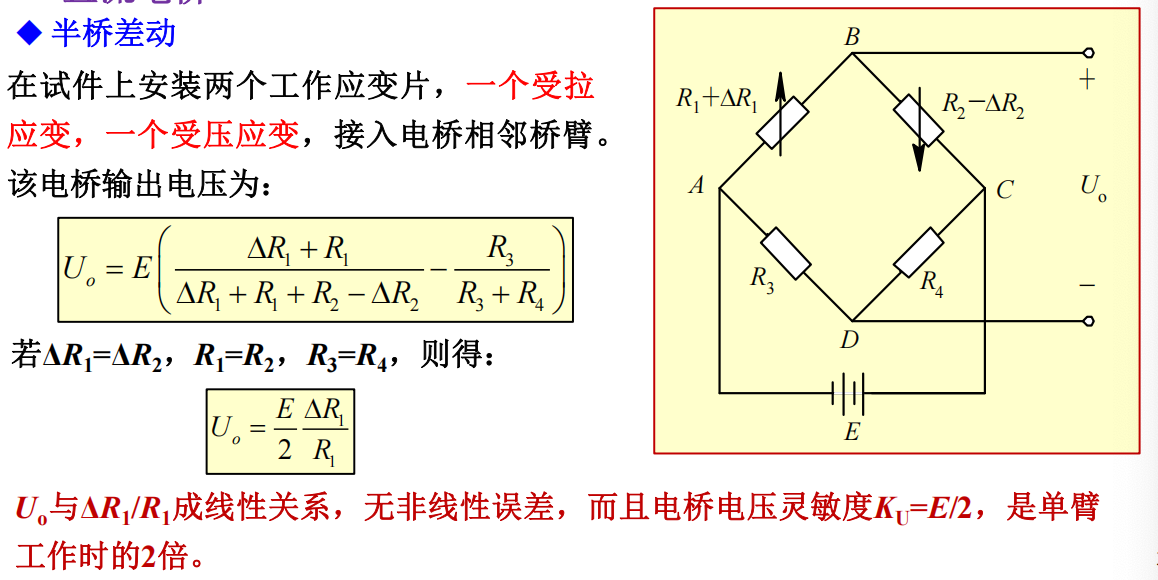
直流电桥输出电压为:
\[U_o = E(\frac{R_1}{R_1 + R_2} - \frac{R_3}{R_3 = R_4})\]平衡条件为:
\[\frac{R_1}{R_2} = \frac{R_3}{R_4}\]定义电桥电压灵敏度为:
\[K_U = \frac{U_o}{\frac{\Delta R_1}{R_1}} = \frac{n}{(1+n)^2}E\]- n:桥臂比,$=R_2/R_1$
- E:电源电动势
当电源电动势确定时,对其求导等于0。得当n=1时,$K_U$为最大值$\frac{E}{4}$,此时$U_o = \frac{E}{4}\frac{\Delta R_1}{R_1}$
非线形误差:
\[\gamma_l = \frac{U_o - U_o'}{U_o} = \frac{\frac{\Delta R_1}{R_1}}{1+n+\frac{\Delta R_1}{R_1}}\]t提高桥臂比,非线形误差将减小
半桥差动和全桥差动:

交流电桥
引入交流电桥的原因:直流放大器易于产生零漂
引入交流电源后,由于应变片引线寄生电容使得桥臂呈现复阻抗特性,相当于两个桥臂各并联了一个电容。

交流电桥每个桥臂的复阻抗:
\[Z_1 = \frac{R_1}{1+j\omega R_1 C_1}\] \[Z_2 = \frac{R_2}{1+j\omega R_2 C_2}\] \[Z_3 = R_3\] \[Z_4 = R_4\]开路输出电压:
\[\dot U_o = \dot U_i \frac{Z_1Z_4 - Z_2Z_3}{(Z_1 + Z_2)(Z_3+Z_4)}\]由电桥平衡条件($U_o= 0$)整理可得:
\[R_1R_4 + j\omega R_1R_2R_4C_2 = R_2R_3 + j\omega R_1R_2R_3C_1\]- 电阻平衡条件:$R_1R_4 = R_2R_3$
- 电容平衡条件:$R_1C_1 = R_2C_2$
电容式传感器
特点:工作可靠、寿命长、灵敏度高、分辨力高、精度高、线形好、性能稳定、重复性好
变磁阻电感式传感器(自感式)
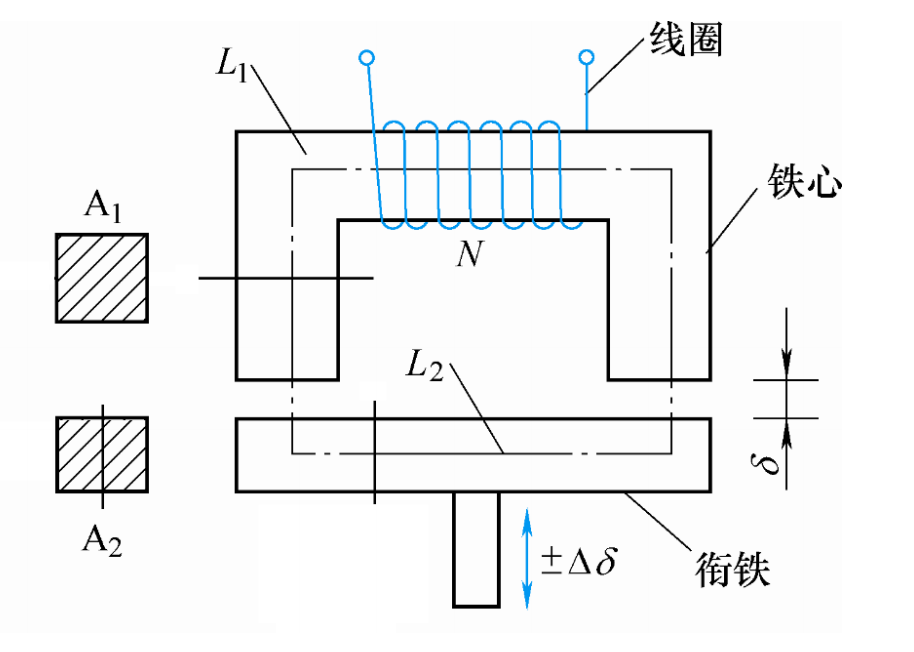
由线圈、铁心和衔铁三部分组成,铁心和衔铁由导磁材料制成
线圈中电感量为:$L = \frac{N^2}{R_m}$
忽略磁路磁损,磁路总磁阻为: \(R_m = \frac{L_1}{\mu_1 A_1} + \frac{L_2}{\mu_2 A_2} + \frac{2\delta}{\mu_0 A_0}\)
其中,
- $\mu_0$:真空磁导率 = $4\pi \times 10^{-7}H/m$
- $L_1/L_2$:磁通通过铁芯/衔铁中心线的长度
- $A_0/A_1/A_2$:气隙/铁芯/衔铁的截面积
- $\mu_0/\mu_1/\mu_2$:空气/铁芯/衔铁的磁导率
- $\delta$:单个气隙的厚度
磁路中的总磁阻近似为:
\[R_m\approx \frac{2\delta}{\mu_0A_0}\]电感量近似为:
\[L = \frac{N^2\mu_0A_0}{2\delta}\]改变$\delta$:间隙变化型传感器;改变$A_0$:面积变化型传感器
衔铁上移,电感总变化量为:$\frac{\Delta L}{L_0} = \frac{\Delta\delta}{\delta_0}$
灵敏度定义:
\[K_0 = \frac{\frac{\Delta L}{L_0}}{\delta_0} = \frac{1}{\delta_0}\]变气隙电感式传感器的测量范围与灵敏度及线性度相矛盾,因此适用于测量微小位移的场合
差动变压器电感式传感器(自感式)
引入原因:减小非线形误差
衔铁上移,电感总变化量为:$\frac{\Delta L}{L_0} = 2\frac{\Delta\delta}{\delta_0}$
灵敏度:$K_0 = \frac{\frac{\Delta L}{L_0}}{\delta_0} = \frac{2}{\delta_0}$
差动式的灵敏度是单线圈式的两倍 差动式的非线性项(忽略高次):$\Delta L/L_0 = 2(\frac{\Delta\delta}{\delta_0})^3$ 单线圈的非线性项(忽略高次):$\Delta L/L_0 = (\frac{\Delta\delta}{\delta_0})^2$ 因此差动式的线性度得到明显改善
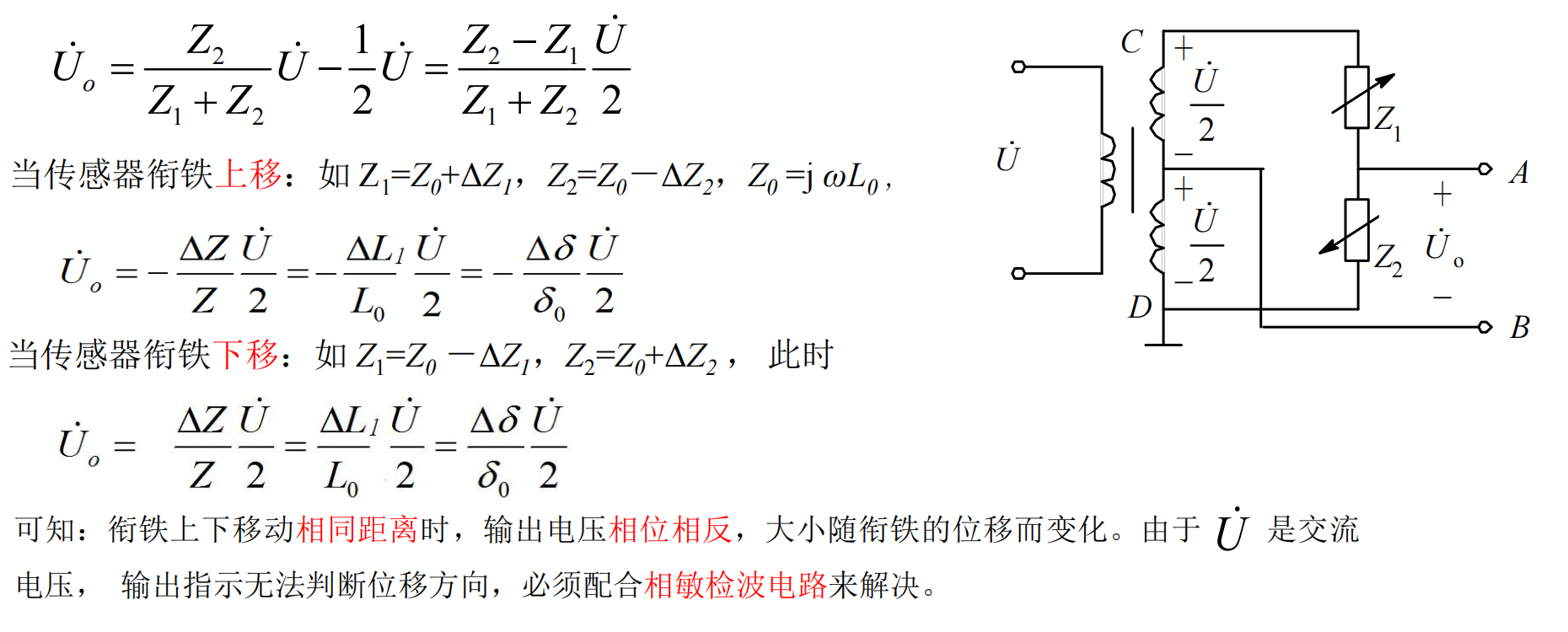
差动变压器电感式传感器(互感式)
- 基本原理:变压器
- 别名:差动变压器/电感式传感器
- 结构形式:变隙式/螺线管式
- 优点:精度高、灵敏度好、结构简单、性能可靠
- 量程:1~100mm机械位移
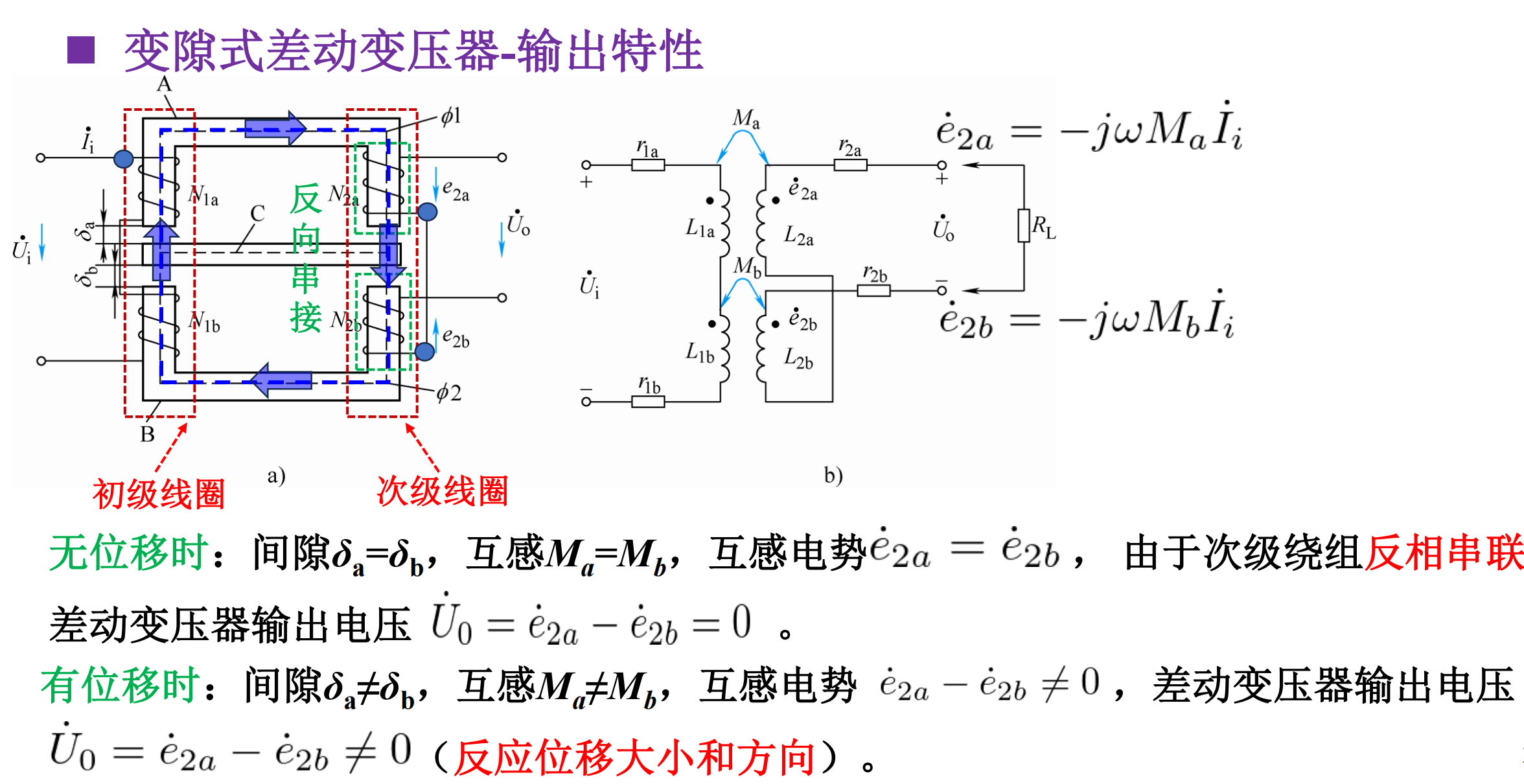
变隙式灵敏度:$K = \frac{N_2\dot U_i}{N_1\delta_0}$
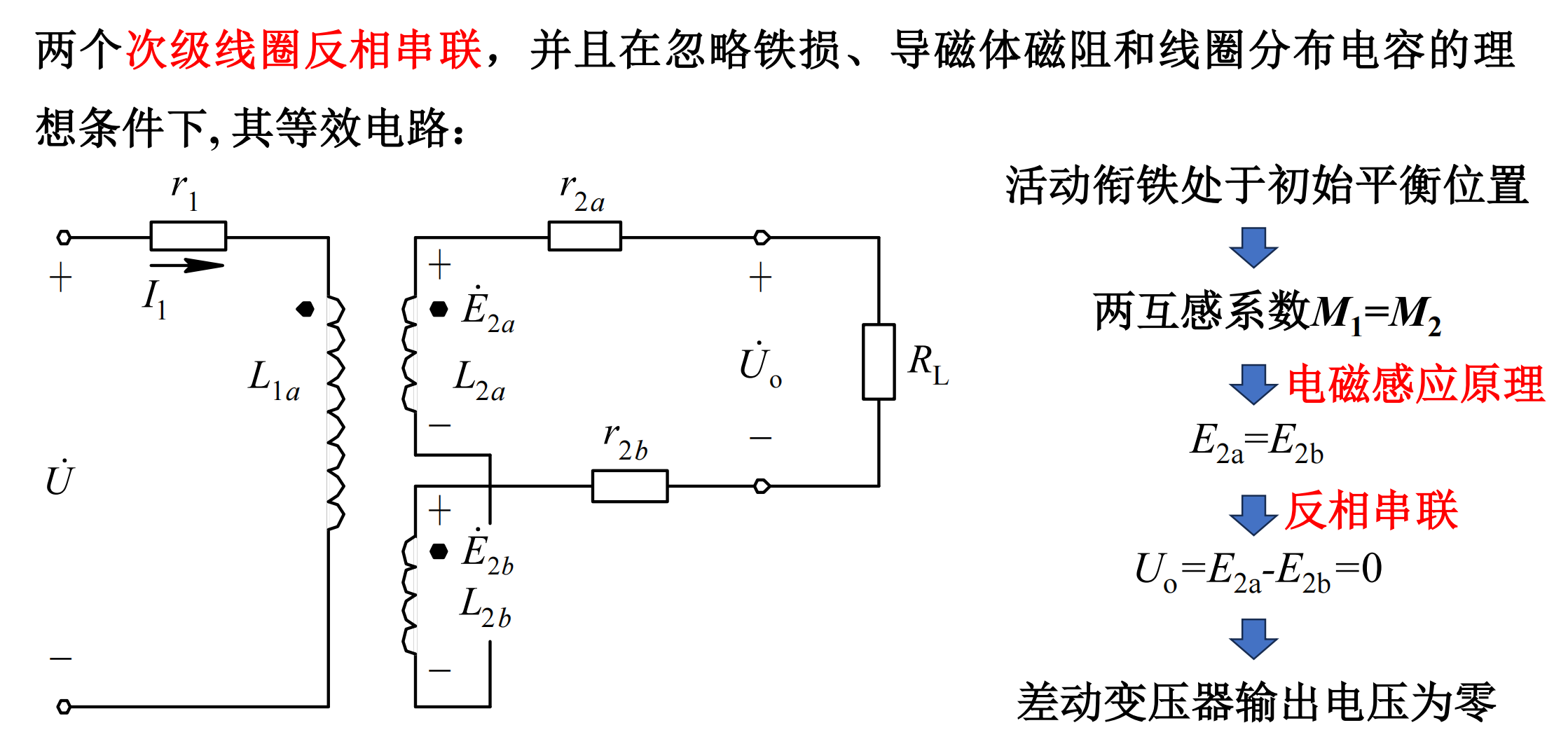
问题:输出的是交流电压(无法表示方向,只能表示大小);测量结果包含零点残余电压。 为了解决如上问题,实际使用差动整流电路和相敏检波电路
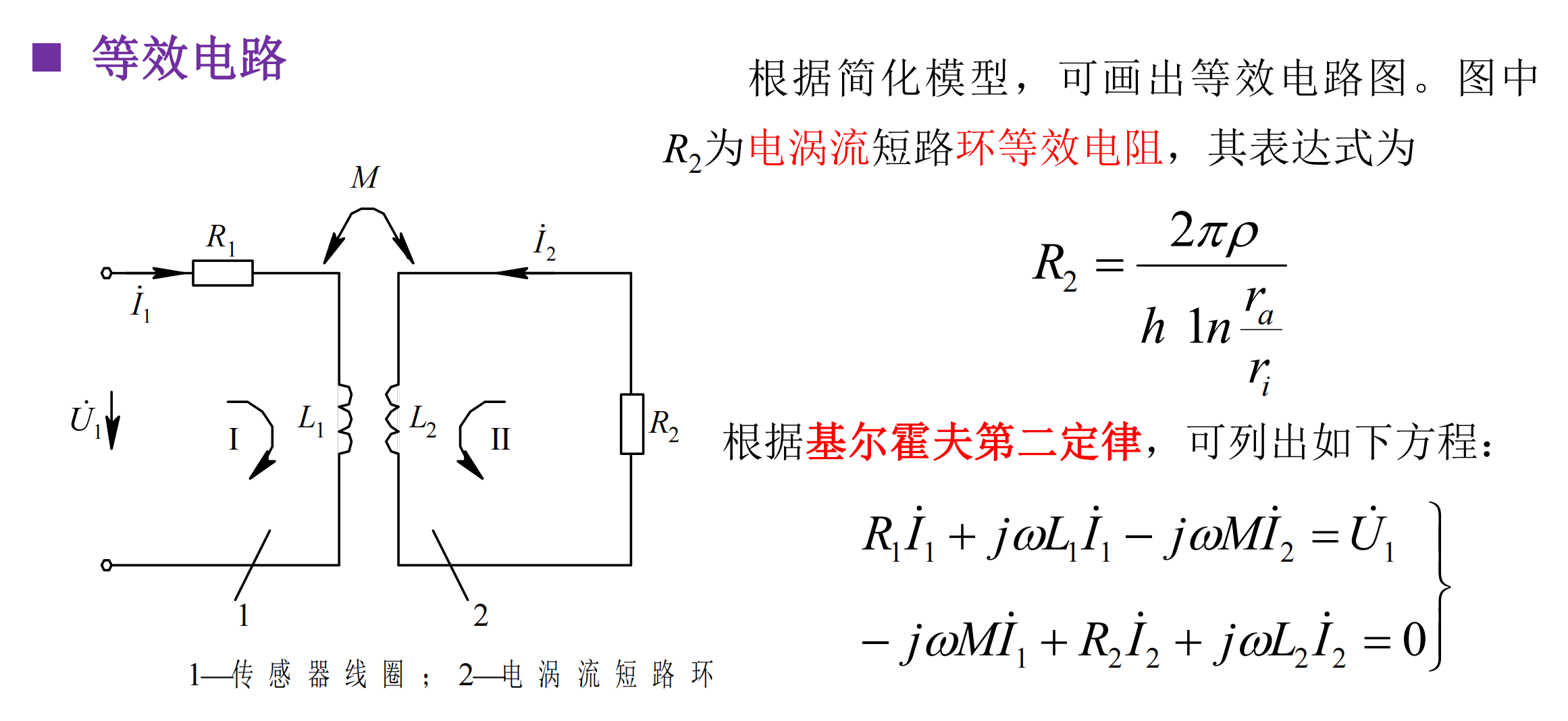
电涡流电感式传感器(互感式)
电涡流效应:当线圈中通有高频交变电流$i_1$时,在线圈周围产生交变磁场$H_1$;交变磁场$H_1$将通过金属导体产生电涡$i_2$,同时产生交变磁场$H_2$,且$H_1$与$H_2$的方向相反;形成$H_2$对$H_1$的反作用,使线圈中的电流$i_1$的大小和相位均发生变化,即线圈中的等效阻抗发生变化,这就是电涡流效应。
- 优点:可进行非接触式测量,结构简单,灵敏度高,抗干扰能力强,不受油污等介质的影响等
- 应用:测量位移、振幅、厚度、工件表面粗糙度、导体温度、材质的鉴别以及金属裂纹等无损检测